Unbelievable study over the last 15,000 years: The mechanics behind the formation of sunspots, coronal mass ejections, coronal holes, and all types of solar storms have been deciphered. The perihelion of Jupiter and Saturn determines their number and size, while the nodal line of Jupiter and Saturn determines their polarity. Miyake events require configurations of the outer planets that enable a long-lasting and uninterrupted flow dynamics from the core to the corona and beyond. All featured by the gravity ramp. – February 12, 2023
In the sun, the gravitational ramp is found in various variations, surrounding the barycenters formed by the Sun and individual planets. It is responsible for the flow dynamics that transport higher temperatures from the core to the shell and beyond. Like the rest of the universe, it behaves in a reactive manner, seeking balance, with cycles lasting up to 1,000,000 years.
By Michael Klejna, still a work in progress V3Rev80.
1. The most important Mechanics and Parameters of Sunspots
1.1. Barycenters
In our solar system, only Jupiter is capable of influencing the Sun strongly enough to cause pronounced surface phenomena, such as sunspots. While most planets share their barycenter with the Sun close to its core, Jupiter’s barycenter with the Sun is, on average, just above its surface at approximately 1.0667 solar radii. Additionally, Jupiter has the strongest gravitational effect on the Sun by far. Thus, the eccentricity of Jupiter’s orbit is the greatest destabilizing factor in the balance of the solar system and the primary factor in the formation of sunspots.
Saturn’s barycenter with the Sun is, on average, 0.5882 solar radii away from the Sun’s core, allowing it to exert its full force within the Sun. In contrast to Jupiter’s barycenter with the Sun, which has over 50% of its area of effect outside of the Sun and the barycenters of the inner planets, their influence is limited to a few hundred kilometers on the side towards the Sun’s core, due to their barycenter being located to close to the core.
Uranus and Neptune appear to have a weak effect, but due to the small distance of their barycenters to the Sun’s core (0.33 and 0.18 solar radii), they have to move much less mass, which might be more viscous due to higher temperatures. Additionally, they fill an important gap between the inner planets, mainly Venus and Earth, and Saturn.
| Constellation to the Sun | Loss due to orbital rotation | Gravity in the barycenter relative to Jupiter’s a (row 2 incl.) | Distance of the barycenter in Sun radii |
| MerkurPerihel | 0,71149 | 3.55% | 0 |
| Merkur a | 0,71149 | 2.24% | 0 |
| Merkur Aphel | 0,71149 | 1.54% | 0 |
| VenusPerihel | 0,88705 | 12.03% | 0,0004 |
| Venus a | 0,88705 | 11.86% | 0,0004 |
| Venus Aphel | 0,88705 | 11.7% | 0,0004 |
| ErdePerihel | 0,93051 | 8.25% | 0,0006 |
| Erde a | 0,93051 | 7.97% | 0,0006 |
| Erde Aphel | 0,93051 | 7.71% | 0,0007 |
| Mars Perihel | 0,96306 | 0.46% | 0,0001 |
| Mars a | 0,96306 | 0.38% | 0,0001 |
| Mars Aphel | 0,96306 | 0.32% | 0,0001 |
| Jupiter Perihel | 0,99414 | 110.53% | 1,0146 |
| Jupiter a | 0,99414 | 100% | 1,0667 |
| Jupiter Aphel | 0,99414 | 90.91% | 1,1188 |
| Saturn Perihel | 0,99764 | 9.9% | 0,5563 |
| Saturn a | 0,99764 | 8.86% | 0,5882 |
| Saturn Aphel | 0,99764 | 7.97% | 0,62 |
| Uranus Perihel | 0,99917 | 0.37% | 0,1716 |
| Uranus a | 0,99917 | 0.34% | 0,1801 |
| Uranus Aphel | 0,99917 | 0.31% | 0,1886 |
| Neptun Perihel | 0,99958 | 0.17% | 0,3287 |
| Neptun a | 0,99958 | 0.16% | 0,3324 |
| Neptun Aphel | 0,99958 | 0.16% | 0,3362 |
1.2. The Significance of Jupiter’s and Saturn’s Perihelion and the Miyake Constellation
Jupiter is responsible for the surface circulation of the Sun and, with its barycenter above the Sun’s surface, is the only external force in the current universe capable of extracting matter from the Sun. Since Jupiter’s perihelion is south of the ecliptic, it is mainly responsible for the formation of sunspots on the southern hemisphere of the Sun.
Saturn, with its barycenter located near half a solar radius from the Sun’s core, acts as a link between Jupiter’s gravity ramp and the gravity ramps of the other planets. This is particularly evident when Saturn is at its perihelion, this is where it most effectively manages to guide near-core flows and thus also temperatures to the outside, enriching Jupiter’s gravity ramp with them. This effect is similar to a turbocharger and sometimes leads to Miyake events. During this event, the Sun rotates in Saturn’s gravity ramp during its perihelion and 60 to 80 degrees later in Jupiter’s gravity ramp, which is then enriched by the already established torsional rotation around Saturn’s gravity ramp.
This constellation, from here on referred to as the “Miyake Constellation”, is about the most optimized flow dynamics from the core to the surface of the Sun, at least Neptune, but preferably Uranus, has to be standing in series with Saturn and Jupiter. At first glance, Earth and Venus appear to have the same force as Saturn, but their barycenters are too close to the core to develop this force. In addition, their gravitational ramps act rather steadily in all directions due to their low orbital periods, it is not possible to form a long lasting stable constellation with them. An absolute minimum for a constellation is 28 days so that the additive effects of a two-time gravitational ramp crossing can build up in the Sun.
In 62018, both Jupiter and Saturn are at their perihelion during this constellation, further enhanced by Uranus, which the Sun rotates into first, providing additional energy from the Sun’s interior and fueling Saturn’s gravity ramp. We should prepare for this stable constellation that occurs approximately every 102,517 years and is expected to be much stronger than the 1944 constellation (here is the link to the representation of the Miyake constellation of 1944 in the Orbit Viewer jsOrrery).
Miyake constellations are primarily responsible for the formation of sunspots on the northern hemisphere of the Sun, as long as Jupiter is north of the ecliptic during the constellation. The angle to the ecliptic is crucial for Earth, determining not only the hemisphere where sunspots form but also whether the maximum of a solar storm, of whatever kind, crosses the Earth’s orbit. The angle to the ecliptic of the individual gravity ramps relative to each other also influences the strength of the overall flow.
Saturn influences Jupiter’s orbit (and vice versa) within a 1% range before, after, and especially during the great conjunction. The effect of this constellation depends on its position relative to Jupiter’s perihelion and aphelion, Saturn can either extend, shorten, affect the distance, or influence it through the addition of its own gravity. These orbit disturbances might extend to the following orbit but are relatively negligible compared to the perihelion-aphelion fluctuations of around 20%. Also, both gravitational axes are almost never congruent, so the individual barycenters and their interaction should usually be used.

1.3. The Gravity Ramp in Detail using the Example of Sunspots
The Sun rotates on its axis every 25.38 days. Taking into account the orbital rotation of the planets, it completes a rotation every 25.38 days plus X days with its entire mass passing through the barycenters it forms with individual planets, thus traversing the gravity ramp (you can find the complete article here: The Gravity Ramp).
The angular momentum of solar particles encounters the gravitation force of the barycenter, which is idealized as radially centric but practically orientates itself at the gravitational axis. This interaction results in internal friction. For rigid elements, this friction transforms into heat, while for viscous elements like in the Sun, it generates a torque corresponding to the decreasing force outward from the barycenter. Additionally, a portion of the intrinsic angular momentum is transferred to the orbital angular momentum of the planet.
If the vorticity arising from the torque within the Sun is significant and enduring enough, it gives rise to another torsional flow, offset by 90 degrees—a suction towards the barycenter within the vortex. Jupiter’s pull towards the barycenter promotes smaller vortices of other planets to the surface, during its maximum this leads to the formation of sunspots. It is highly plausible that Jupiter’s pull is also responsible for coronal holes at the equator during periods of maximum solar activity. The lower temperature and 100 times lower density within a coronal hole support this hypothesis.
2. Cycles
2.1. Short-term Cycles
2.1.1. Cycles of Twelve to Twenty Years
Thus, the short-term cycles of sunspots are explained, each being a product of the interplay of Jupiter’s nearly twelve-year orbital period, the 20-year period of the grand conjunction or its transition into the Miyake constellation, and hence, the staggered Jupiter/Saturn constellations, in relation to the number of spots and intensity of solar activity.
These cycles are also influenced by the alternation between ascending and descending deflection approximately every 15 years, corresponding to Saturn’s half-orbital period, in competition with Jupiter’s ecliptic inclination following its 12 year cycle, thereby determining the North/South distribution.
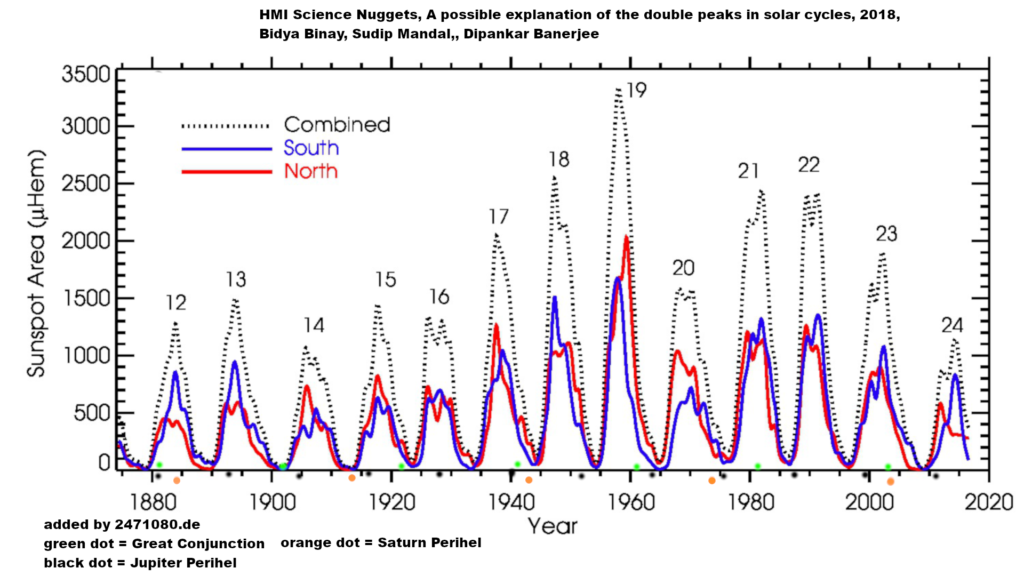
2.1.2. Cycles of 60 to 600 Years
The great conjunction or its transition into the Miyake constellation moves in comparison to Jupiter’s perihelion. In a 60-year cycle, one of the three major conjunctions or their transition into the Miyake constellation, during which Jupiter’s perihelion (this also applies to Saturn’s perihelion) is closest, occurs.
At present, there is less than 90 degrees between Jupiter’s and Saturn’s perihelia. If the great conjunction occurs between them or directly at Jupiter’s perihelion, most sunspots are formed.
If several consecutive 60-year cycles occur in this range, we are in a warm period. If there are no cycles in this range consecutively, we are in an ice age concerning the short-term sunspot contribution to the climate (this, according to a cautiously estimated guess, should be around 0.5°C).
Calculating precisely with 19.859 years between great conjunctions and 29.457 years per Saturn revolution, a cycle lasts 585 years. This cycle includes three maxima and three 40-year jumps during the transition from the main conjunction to the following one. The perihelion wander is not taken into account.

2.1.3. 900-Year Cycle
A 900-year trend is determined by Uranus with its maximum approach to the great conjunction or its transition into the Miyake constellation within this period, again in relation to Jupiter’s and Saturn’s perihelia.
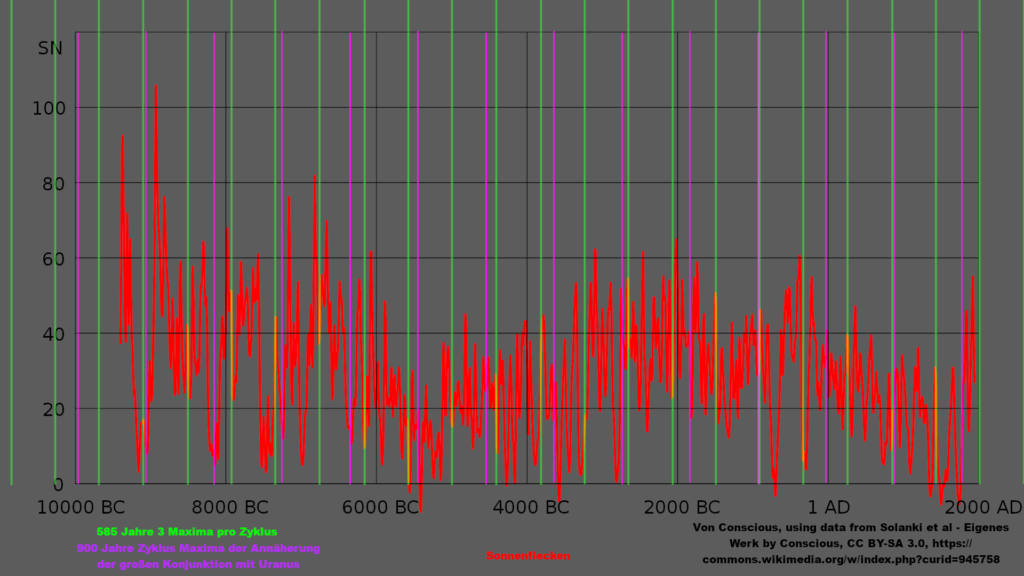
2.2. Long-term Cycles
2.2.1. 100,000-Year Cycle
The long-term cycles of sunspots are primarily determined by the perihelion wander. When Jupiter unfolds only 90.88% of its average gravitational effect on the Sun in the aphelion, it becomes 110.53% in the perihelion. If Jupiter’s and Saturn’s perihelia align at the same angle to the Sun, it reaches 120.48%, equivalent to 132.57% of the minimum, occurring in a cycle of approximately 102,507 years, consistent with climate parameters from ice core drillings.
The Earth’s perihelion has its greatest proximity to this 102,507-year cycle in a 1,122,000-year cycle. Hence, every 1,122,000 years, the maximum solar activity coincides with the Earth’s maximum approach to the Sun.
2.2.2. 400,000-Year Cycle
Approximately every 417,000 years, there is an almost triple perihelion conjunction of Jupiter, Saturn, and Uranus. This is responsible not only for the number of sunspots but also for the maximum eccentricity of the Earth’s orbit.
3. Conclusions
Even in the self-dynamic interior of a star, the torque of the gravity ramp can prevail against thermodynamic processes and superrotation caused by Sagittarius A*, as well as it can against superrotation on Jupiter and its energy-intensive processes. Understanding this fine mechanic of balance in celestial mechanics and its responsibility for magnetic fields, atmospheres, and radiation is strongly adviced. Therefore it should be calculated precisely.
3.1. The Gravity Ramp in Stars and Planets
If the gravity ramp is well understood, it can be used to calculate radiation conditions in other star systems, especially in binary star systems with hot Jupiters. It can serve as a parameter for determining the habitable zone.
If the gravity ramp is well understood, it can be used to calculate how large a moon must be to create stable, Earth-like conditions on a planet in the habitable zone, concerning magnetic fields and atmosphere.
Is there enough matter in the solar system to transform Mars into a small Earth with the help of a moon? The answer is yes; the matter is scarce, it requires a lot of work and takes hundreds of years, but yes, we could create a second planet that, thanks to the gravity ramp, would have a technically independent and stable Earth-like climate (you can find the complete article here: The Path to Interstellar Society).
3.2. Climate and Milankovitch Cycles
If the gravity ramp is well understood, climate fluctuations caused by it can be calculated in advance.
The eccentricity of the Earth’s orbit as a parameter in Milankovitch cycles is incorrect. The cycles used under eccentricity are based on the mechanisms of solar activity. The perihelion migration of the Earth does not match that of Saturn. If there were a relation to Jupiter’s perihelion migration, the cycle would be 331.000 years. Additionally, there should be a distinct 20-year cycle in the solar radiation data that deviates from the sunspot count because the orbit disturbance caused by the great conjunction shifts 120 degrees every 20 years.




