This article explains the main parameters and their functioning based on the internal friction of angular momentum and gravity in the barycenter, arising from the rotation of the central body relative to its gravitational reference systems, as well as their effects: planetary magnetic fields, atmospheres, and superrotation.
by Michael Klejna, still in progress, V3R38
Table of Contents
1. The Gravity Ramp
The fundamental condition for the existence of a gravity ramp is a two- or multi-body system.
1.1. Functioning of the Gravity Ramp
1.1.1. Rotation in Relation to the Gravity Axis
In the following two cases, the central body rotates in relation to the common gravity axis with another body on which the gravity ramp also lies.
By rotation, we usually mean the angular momentum, that is, a rotating central body orbited by one or more bodies (e.g., the Sun & Jupiter), or in exceptional cases, two bodies orbiting a fixed body at different speeds and overtaking each other (orbital angular momentum). Here, one could speak of indirect rotation since the bodies do not necessarily have to rotate around themselves. This indirect rotation is responsible, for example, for the volcanic activities and atmospheres of the Galilean moons. With bound rotation, the angular momentum corresponds to the orbital angular momentum, thus there is no rotation in relation to the gravity axis.
1.1.2. Gravity Axis and Barycenter
The gravity axis between two bodies runs in a straight line between their centers of mass. Most stars, planets, and moons are spherical, with their density increasing towards their centers, thus having a core that represents a high proportion of the total mass. Gravity is strongest along the axis between their centers and specifically at the barycenter, the common center of mass of both masses, and decreases with increasing distance from there.
The distance of the barycenter on the gravity axis from the core of the rotating central body increases with the mass of the second body. The gravitational force at the barycenter is determined by the product of the masses of both bodies and their distance.
1.1.3. Tidal Forces and Internal Friction
Tidal forces (e.g., Earth/Moon & tides) act on a body that rotates in relation to one of its gravitational axes. Tidal friction occurs, causing the rotation of the central body to decrease and the orbit of the orbiting body to increase (when the angular momenta are in the same direction).
This tidal friction is strongest during the crossing of the gravity axis. In detail, the mass of the rotating body experiences different gravitational forces while crossing the gravity axis. In other words, the angular momentum of the central body encounters the forces acting at the barycenter.
Depending on the viscosity of the material at the barycenter, it is heated by frictional pressure or experiences torque, usually a combination of both. This flow equilibrium is mainly influenced by the elliptical orbits, in multi-body systems also by resonance effects and disturbances caused by certain constellations.
If there is torque at the gravity ramp, a vortex forms north and an opposing vortex forms south of the gravity axis (To understand, imagine your leg as the gravity axis and place it in a river, the water corresponds to the rotating mass.).
If the barycenter lies within the radius of the rotating central body, the gravity ramp there is steepest at right angles to the gravity axis. If the vortex is stable and strong enough for long enough, it forms the bottom of a whirlpool. This whirlpool is a torsional flow offset by 90 degrees from the vortex flow along its longitudinal axis.
1.1.4. Multiple Crossings of the Gravity Ramp
This effect of the gravity ramp repeats with each rotation; depending on the position of the barycenter, a vortex with outward suction (e.g., sunspots due to Jupiter) or inward suction (e.g., Jupiter’s Great Red Spot due to the Galilean moons) is created.
During a full rotation of the central body, the torque gained at the gravity ramp decreases. If there is residual torque upon crossing the gravity ramp again, the following occurs:
The horizontal impulses add up forming two equatorial bands, with opposing boundaries, which because of their positions north and south of the gravity axis rotate in mirrored directions.
While the vertical impulses partly have negative effects, the difference between positive and negative effects determines the width of the bands, thus their permeability and to what extent a torsional rotation can develop around both bands.
With multiple crossings of the gravity ramp and rigid materials, their effect builds on the possibly still remaining residual heat of the material from the previous crossings of the gravity ramp.
1.1.5. Position of the Barycenter relative to the Central Body
If the barycenter lies within the radius of the central body, friction increases the further the barycenter is from the rotational axis of the central body, as the distance from the rotational axis also increases the angular momentum of the rotating particles.
If the barycenter is far from the central body, the gravity ramp, acts horizontally, if it exists at all, as it loses strength with increasing distance.
1.1.6. Interaction of Multiple Gravity Ramps in a Central Body
In a pure two-body system, such as Earth and the Moon, the effects of the gravity ramp are stable and balanced. In multi-body systems, new constellations constantly arise, with the flows of the gravity ramps influencing each other through resonances or disturbances, thus presenting a chaotic overall picture. The two most prominent variants in the solar system are:
The multi-body system consisting of the Sun and its planets, where the barycenters with respect to the distance from the solar core are widely distributed and can thus form a chain from the core to beyond the surface. The more links this chain has, the stronger it is, and the rarer it occurs; it also requires long-lasting constellations to build up. Furthermore, it is very susceptible to disturbances; as soon as one link acts in the wrong direction, it completely collapses.
In contrast, the multi-body system consisting of Jupiter and the Galilean moons, which, due to the similar forces and core distances of their barycenters, ensure a rather constant flow by constantly refreshing the torque. Compared to the two-body flow, this gravity ramp ring still has resonance maxima and disturbance valleys but is simultaneously more stable than a gravity ramp chain, like the one the influences of the planets on the Sun can form.
1.1.7. Other Parameters Influencing Flow Dynamics
A high inclination of the rotational axis of the central body results in significant efficiency losses when the orbit of the second body is oriented to the ecliptic plane of the central body. Similarly, a high orbital inclination of the second body relative to the central body’s orbit reduces efficiency. It is very helpful for visualization to observe how the gravity axis between the Earth and the Moon wanders over the Earth’s surface from the Moon’s perspective (Here is the link to the Orbit Viewer jsOrrery with the corresponding settings).
1.1.8. The Gravity Ramp in Practice Using Jupiter as an Example
Jupiter receives only 3.7% of the sunlight compared to Earth. A Jupiter day lasts just under ten hours. Jupiter has no crust; its surface is not divided into land and water. The inclination of its rotational axis is only 3 degrees, not 23 degrees like Earth’s.
Consequently, there are no seasons, no day/night or land/sea temperature differences, hence no reason for weather comparable to that on Earth. And yet, the Great Red Spot is described as the largest storm in the solar system.
The visible currents on Jupiter’s surface originate deep within Jupiter and reflect the torques that arise when Jupiter rotates over the gravity ramps it forms together with the Galilean moons.
The Great Red Spot is the result of a triple conjunction of the Galilean moons, either overlapping three gravity ramps and adding up to a common one or distributing them so evenly that the highest possible continuous torque is guaranteed. This constellation occurs approximately every 300 Jupiter days, seemingly synchronizing temporarily with Jupiter’s rotation period, making it possible to maintain the torque and thus the Great Red Spot for many years.

2. The Effects of the Gravity Ramp
2.1. The Ring Magnet Model – How Planetary Magnetic Fields are Strengthened by the Gravity Ramp
The magnetic field component generated by the gravity ramp of a planet arises from the rotation of vortices formed north and south of the gravity axis during the crossing of the gravity ramp, within the magnetic remanence of the central body.
If the flows of these vortices remain stable during a complete rotation of the central body, two ring magnets form around the core of the central body. These ring magnets are separated by the gravity axis and, like the vortices, are polarized differently. They harmonize with the magnetic remanence of the central body, thus enhancing the planetary magnetic field particularly in the equatorial plane or along the gravity axis.
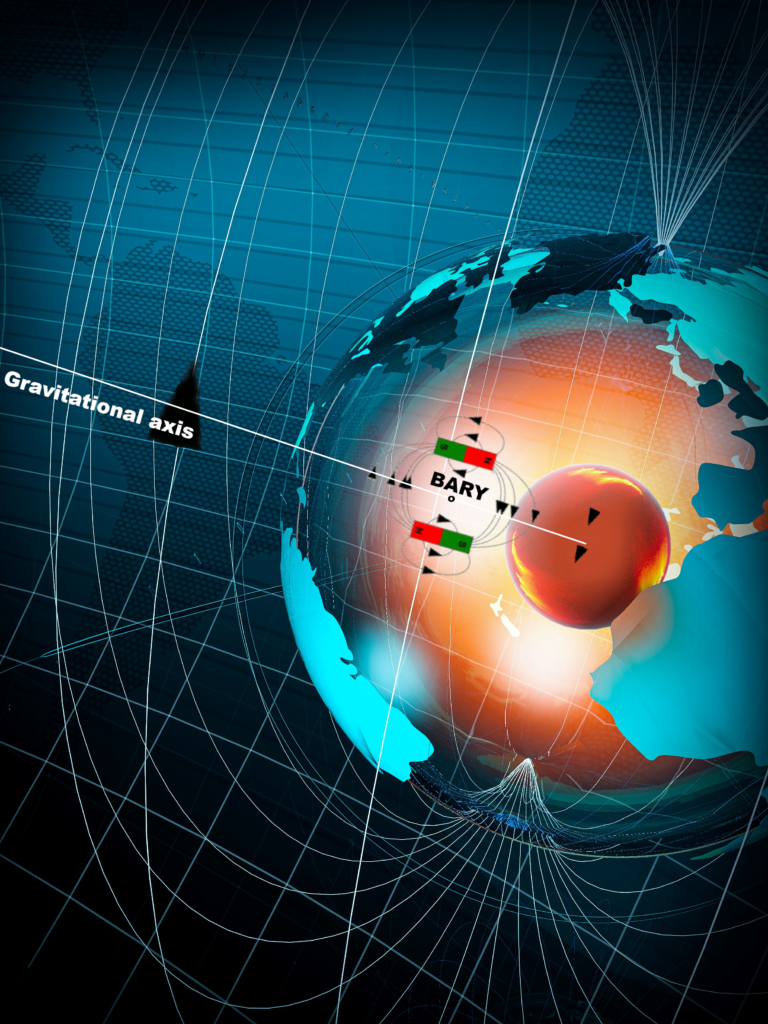
If you mentally multiply the following ecliptic and axis values of the Earth, Moon and Sun (Fig. 2) by the depicted gravity ramp mechanics (Fig. 1), you get the influence of the Moon and the Earth’s rotation on the Earth’s magnetic field, as shown in the following Figure 3.


2.2. The Gravity Ramp and Atmospheres
By tidal forces in general and the gravitational ramp’s torques additional temperature and pressure differences do start more chemical processes compared to a non-rotating body, which is resting in balance.
Newly created elements diffuse, the heavy ones towards the core, the light ones outwards, building up an atmosphere.
How much a body was exposed to this process could be reconstructed by analyzing the size of its core (e.g. Mercury), also conclusions about its former rotational speed could be drawn (see also Pluto & Charon).
To keep up an extensive atmosphere a magnetic field is necessary as sun wind guard. Whereby an indirect magnetic fields inside the field of a dominant body makes it harder to keep light elements, compared to a direct one.
If a planet is able to build a stable, dense atmosphere is not only a question of its mass. It’s more like one of its balance of production and loss of light elements.
2.3. The Gravity Ramp and Superrotation
When a body is in a constellation that consolidates all the gravitational axes influencing it on one side, superrotation occurs on the opposite side. This can be observed well in Jupiter’s Great Red Spot; it grows during these phases and appears to move forward. Its growth is a result of the addition of gravitational axes, and what moves forward is merely its surface manifestation, driven by increased superrotation.
Polewards, the superrotation decreases, also because the equatorial suction of matter forms a countercurrent as a source of matter at the poles. Equatorially, superrotation can amplify the effects of the gravitational axis transition as it increases angular momentum.
3. The Life Vector in the Two-Body System
The life vector is the isolated force behind the gravitational ramp.
4. Proportion of the Coriolis Force
The primary deflection direction at the gravitational ramp is northward or southward along the gravitational axis, i.e., parallel to the rotation axis, and thus not relevant for the Coriolis force. Any movement at a differing angle is partially distorted by the Coriolis force, which makes recognizing the mechanics at the surface more difficult.






















